Highlight activities
Project Outline
This project focuses on coupled-physics impedance tomography with
hybrid data. We will derive and compare constructive formulations of the
underlying problems, formulate mathematical algorithms for their solution,
and rigorously prove fundamental properties of the algorithms and the solutions.
In addition, we will develop state-of-the-art numerical reconstruction
algorithms for the problems, and we will find ways to incorporate prior
information about the solution to obtain regularized reconstruction
methods whose solutions are robust w.r.t. to data errors.
We will approach a number of important theoretical questions related
to impedance tomography via hybrid data, with focus on CDII and UMEIT
problems. These questions are primarily connected to the underlying PDE
formulations, the associated variational formulations, and how to
impose stability by means of data fitting and prior information.
We are not concerned with the problems of building the devices and
performing the measurements; for test and validation we will use
artificial data created through numerical simulations.
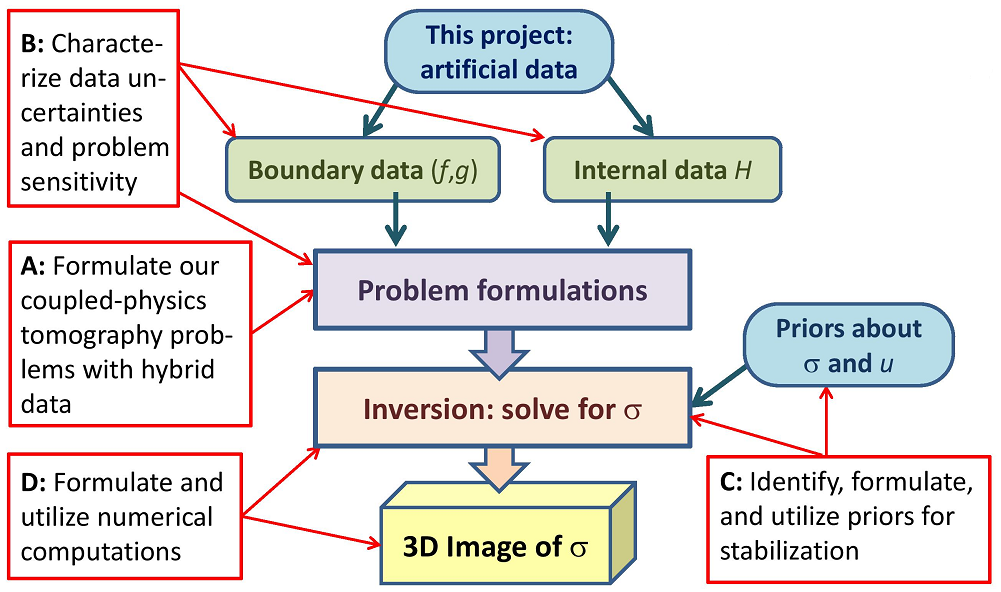
The project has considered the following questions related to tomography
problems with hybrid data:
-
Among different formulations of the inverse problem (including PDE
formulations and variational formulations), which ones have favorable
theoretical properties?
-
To which extent can we state and prove results about the solvability
of the variational problems and the properties (existence, uniqueness, etc.)
of their solutions?
-
How can we characterize the uncertainties in the data?
This covers both the directly measured electric boundary data
(f,g) and the internal data H.
-
Which types of prior information are relevant for these problems,
and how do we characterize this information in a way that allows us
to incorporate it in the inverse problem?
-
How do we take account of the data uncertainties and, at the same time,
incorporate the given prior information about the solution to stabilize
the solution?
-
What are the most efficient algorithms for solution of the problems
in 2D and 3D?
-
How can we best utilize computational experiments (using artificial data)
with different types of formulations, noise levels, and priors to verify
our theoretical results?