Scientific Machine Learning

Scientific machine learning is a subfield of Artificial Intelligence and constitues computional techniues and technologies grounded in scientific approaches that via algorithms learn from data to augment or automate human skills and insights. The adoption of scientific machine learning is transformational across science and engineering and enable explainable predictive modelling and learning from data and seek to secure robustness and reliability for practical use cases via proper use and design of algorithms. Many new capabilities are offered for solving complex problems relying on data, utilize mathematical modelling and domain expertise, employing mathematical optimization and using proper design of powerful computational processes.
Scientific Machine Learning brings many opportunities for advancing industrial applications, data-driven ressource optimization and digital innovation related to Internet of Things, Digital Twin concepts, Acceleration of advanced simulations, Design Optimization workflows, Visual Computing, Accelerated simulations, etc.
Mission
The improvement or replacement of dedicated simulations by data-driven methods and guided by physical measurements, by low-rank approximations and by reduced modeling strategies combined with high performance computing approaches is an active field of research that is quickly finding its way into industrial applications. To address this, the objective is to research, improve, develop and apply fast and efficient state-of-the-art data-efficient numerical algorithms, based on machine learning (ML) and scientific computing (SC). The methods should be robust, reliable, scalable and fast on modern computing systems to solve high-dimensional problems, utilize uncertainty quantification, mathematical optimization, model-based simulation, take into account measurements, machine learning / artificial intelligence and surrogate modelling utilizing high-performance computing. The research focus on theoretical developments as well as practical applications via software development and open source frameworks. The impact of methods and their applications within sustainability is considered.
Applied Artificial Intelligence / Scientific Machine Learning
- The AI Denmark initiative directed at practical use cases is supported.
- The Danish Data Science Academy (DDSA) initiative directed at growing a strong data science comunity in Denmark is supported.
Events
- PhD school 02901 Advanced Topics in Machine Learning: Physics meets Machine Learning, August 19-23, 2024
- HAMLET/Physics 2024 - How to Apply Machine Learning to Experimental and Theoretical Physics, August 19-21, 2024
-
Danish Digitalization, Data Science and AI - D3A 1.0, 1-2 Feb, 2024
with a session on "Deep Learning in Science & Physical Systems", including talks on "Scientific Machine Learning for Computational Science and Engineering Applications" by Allan P. Engsig-Karup (DTU Compute). -
Mathematics of Data Science seminar series, supported by DDSA.
- Jan S. Hesthaven, Enabling digital twins through modeling, data, and learning â a few examples , May 17th, 2024
- Dirk Hartmann, Executable Digital Twins, Feb 6, 2024
- Esteban Ferrer, New avenues in high order fluid dynamics, June 16, 2023
- Gianluigi Rozza, Reduced Order Modelling in Computational Mechanics: state- of the art, challenges and applications, March 7, 2023
- George Em Karniadakis, Physics-informed machine learning: blending data and physics for fast predictions, November 9, 2022
- DTU Compute special course on "Data-Driven Science and Engineering", Feb - Jun, 2023, new course developed by Allan P. Engsig-Karup
- 2022 Sep - 2023 Feb, DDSA Mentoring Programme - Pilog Mentoring Programme
- DTU Compute PhD school on "Scientific Machine Learning", June 13-17, 2022, cf. DTU Course 02977. The course is supported by DTU Compute PhD school, Danish Data Science Academy (DDSA), DCAMM, EUROTECH and CERE.
-
DTU Compute SciML Lunch Seminar 8/3-2022 12:00 - 12:45:
"Markov Chain Generative-Adversarial Neural Networks for
Solving Bayesian Inverse Problems" by Nicolaj Takata
Mucke
Recording: LINK - DCAMM Annual Speaker 2022 "Physics-Informed Machine Learning: Blending data and physics for fast predictions", George Em Karniadakis, Brown University, USA (November 10, 2022)
-
2022-2023 Inspirational seminar series on Mathematics of Data
Science supported by Danish Data Science Academy (DDSA) and Danish
Center for Applied Mathematics and Mechanics (DCAMM)
- November 9, 2022, Prof. George Em Karnidakis: "Physics-informed machine learning: Blending data and physics for fast predictions"
Study group
- We form study groups every semester on the topics of Scientic Machine Learning that is rapidly evolving. Drop an e-mail if you are interested to take part and contribute.
- Workshops DTU Environment/DTU Compute : Hydraulic Modelling (Since Autumn 2021)
Examples of Application Areas
 | Dynamical systems and scalable simulations |
 | Design optimization |
 | Real-time prediction |
 | Physics-informed surrogate modelling for acceleration |
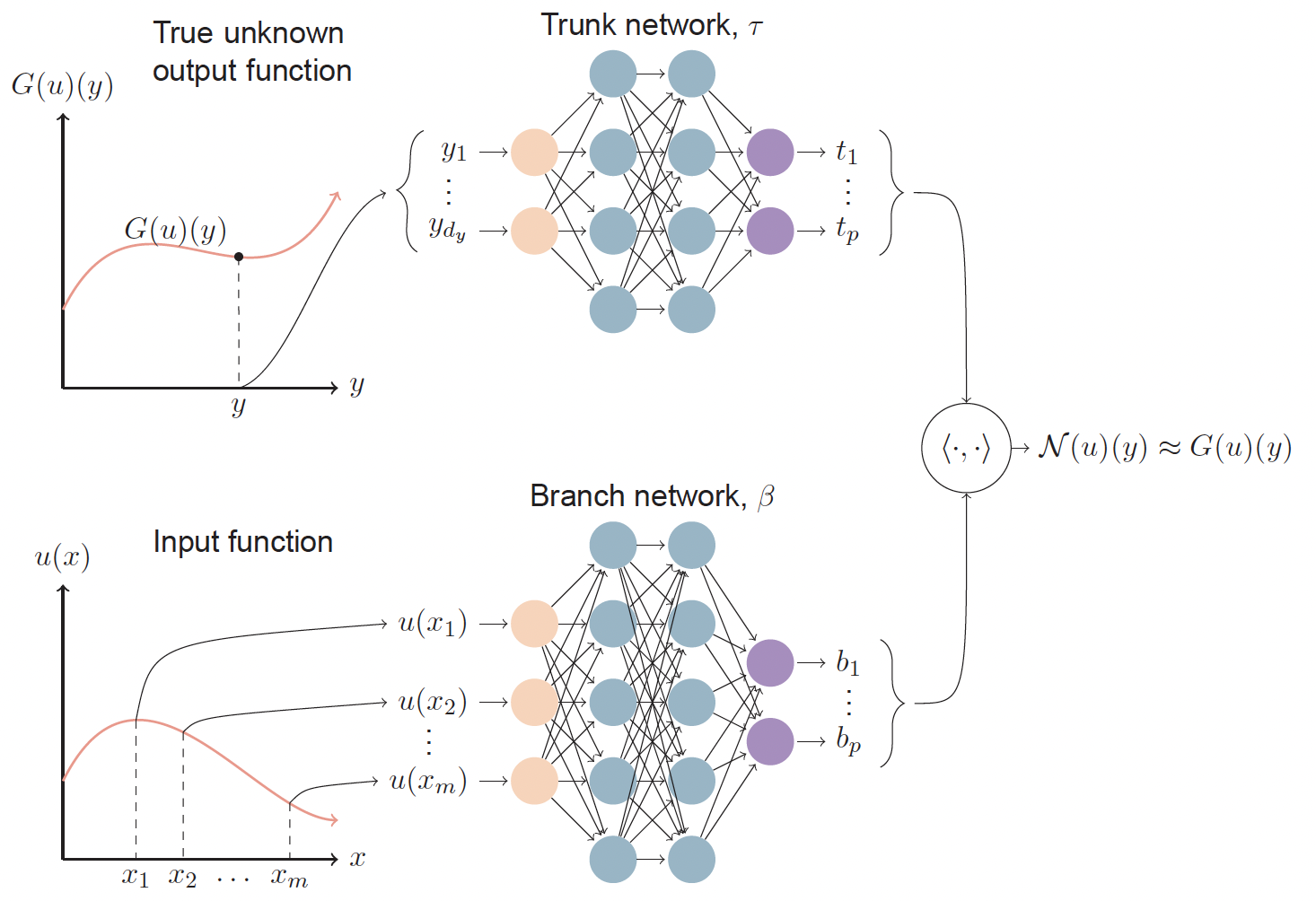 |
Accelerated computing using operator learning |
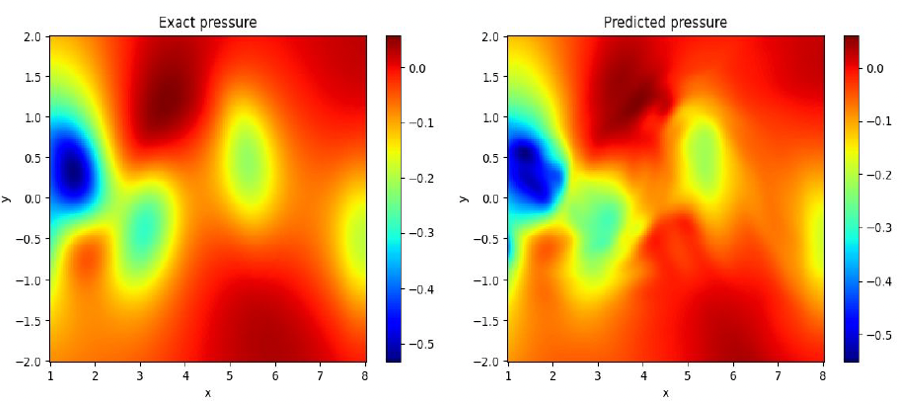 |
Physics-informed Generative learning and data generation for nonlinear dynamical systems |

|
Uncertainty quantification and uncertainty-aware acctive learning for engineering systems |
Recent student research projects
- Physics-Informed Neural Networks for Solving the Linear Elasticity Equations in Continuum Mechanics (MSc, Feb-Jul, 2024)
- Fourier Neural Operator-Driven Multi-Fidelity Surrogate of RANS-based Wind Farm Wake Simulations (MSc, Feb-Jul, 2024)
- Numerical solutions of PDE’s assisted by Neural Networks (Minor project, Feb-Jun, 2024)
- Integration of Scientific Computing Agents in LangChain Powered by Language Models (Minor project, Feb-Jun, 2024)
- Comparative analysis of deep learning based sound event detection methods in the urban environmental audio domain (MSc, Feb-Jul, 2024)
- Fidelity Enhancement of Wind farm wake simulations using the Fourier Neural Operator (MSc, Jan - Jun, 2024)
- Data-driven surrogate models for physics-based numerical models (MSc, Sep, 2023 - Feb, 2024)
- Predicting bacterial infections using machine learning (MSc, Aug, 2023 - Mar, 2024)
- Physics-informed Neural Networks for Wind Turbine Wake flow predictions (Special course, Sep - Dec, 2023)
- Reduced order modelling for computational engineering (Special course, Feb - Jun, 2023)
- Augmenting a Neural Operator with the Finite Element Method to Develop a Hybrid PDE-solver (Special course, Mar - Jun, 2023)
- Machine learning methods for modelling of dynamic systems (MSc thesis, Feb - Sep, 2023)
- Uncertainty Quantification in Machine Learning models using Conformal Prediction (BSc thesis, Feb-Jun, 2023)
- Machine Learning for UneXploded Ordinance (UXO) Detection from drone surveys (BSc thesis, Feb-Jun, 2023)
- Automating solar panel fault detection from image data (BSc thesis, Feb-Jun, 2023)
- Data-driven techniques for learning nonlinear dynamics of physical systems (M.Sc., Aug 2022 - Jan 2023)
- Dynamic 2D flood simulations using scientific machine learning (MSc., Aug 2022 - Feb 2023)
- Data-driven Neural Operator Techniques for Efficient Surrogate Modelling (M.Sc., Aug 2022 - Jan 2023)
- Using data-driven state-of-the-art machine learning and conformal prediction for track irregularities from observed dynamics of in-service railway vehicles (M.Sc.,Feb- Aug, 2022 )
- Neural Operators (Special course, Jun-Jul, 2022)
- Variational Auto Encoders (VAE) for Differential Equations (Special course, Jun-Jul, 2022)
- A neural operator for solving the wave equation (Special course, Sep-Dec, 2022)
- Scientific machine learning for discovering basal dynamics of Greenland outlet glaciers (M.Sc., Jan - Aug, 2022)
- Surrogate Modelling for Estimating Sound Speed Profiles (PhD special course, Feb - May, 2022)
- Physics-informed data-driven techniques for parameter estimation and discovery of hidden physics with application to models for spread of diseases (special course, Sep - Dec, 2021)
- Physics-Constrained Surrogate Modelling for Computational Hydraulics (M.Sc., Sep 2021 - Feb 2022)
- Acceleration of Physics-Informed Neural Networks (B.Sc., Sep - Dec, 2021)
- Physics-Informed Neural Networks for Solving Coupled Partial Differential Equations (special course, Aug 2021)
- Mathematical modelling of Covid-19 epidemic (B.Sc., Feb - June 2021)
- Mathematical modelling of Covid-19 (B.Sc., Feb - June 2021)
- Finite Element Method for partial differential equations - Discovey of Advection Equation (Special course, Feb 2021)
- Scientific Machine Learning (Special course, Feb - Jun 2021)
- Physics-informed Neural Networks (Special course, Sep - Dec 2020)
- Predictive Maintenance of Ship Engines using Machine Learning (M.Sc., Apr - Sep 2020)
- Machine Learning for matching transaction data with invoice data (B.Sc., Apr - Sep 2020)
- Drag loss for wave-body interaction (Minor, Jun 2020)
- Machine Learning for Predictive Root Cause Analysis in Log Data in an Enterprise (B.Sc., Feb - Jun 2020)
- Sparse Grid Methods for High Dimensional Function Approximation (M.Sc. Project, Feb 2019 - July 2019)
- Music Composing with Artifical Intelligence (Minor project, Feb 2019 - June 2019)
- Optimal Control of Nonlinear PDE Systems Using Reduced Order Modeling and Neural Networks (M.Sc., Aug 2018 - Jan 2019)
- Numerical Solutions to Nonlinear Partial Differential Equations via Physics-Informed Neural Networks (B.Sc., Feb 2018 - Jul 2018)
- Reduced Basis Methods for parametrized PDEs (Special, Oct 2017 - Jan 2018)
- Applied Machine Learning for Prediction (Project, Sep 2017 - Dec 2017)
- Function approximation using Artificial Neural Networks (B.Sc., Feb 2017 - Jun 2017)
Courses with Scientific Machine Learning content

- 01666 Project work - Bachelor of Mathematics and Technology
- 02456 Deep Learning, project work
See posters via the link. - 02623 Finite Element Method of Differential Equations
- 026XX Data-Driven Computional Science and Engineering (since 2023)
- 02687 Scientific Computing for Ordinary and Partial Differential Equations
- 02689 Advanced Numerical Methods for Differential Equations
- 02977 Scientific Machine Learning
Peer-Reviewed Publications related to data-driven methodologies, analysis and science and engineering applications
- Data-driven Multi-Fidelity Modelling for Time-dependent Partial Differential Equations using Convolutional Neural Networks (May, 2024)
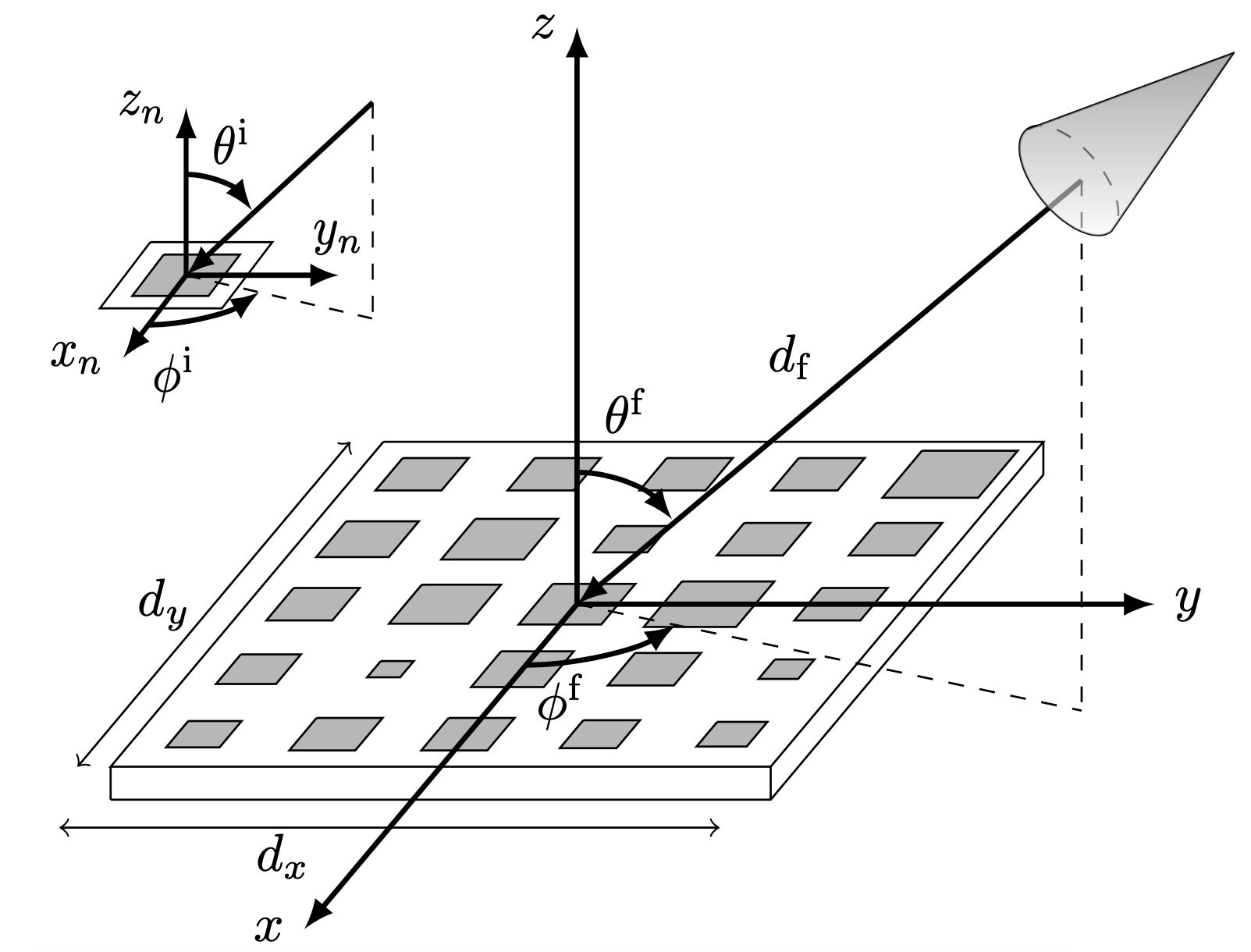
- Sound propagation in realistic interactive 3D scenes with parameterized sources using deep neural operators (Jan, 2024)
- Improving Deep Learning-Based Defect Classification in Solar Cells Using Conformal Prediction (Jun, 2023)
- Reduced order modelling using parameterized non-uniform boundary conditions in room acoustic simulations (Apr, 2023))
- Efficient Uncertainty Quantification and Variance-Based Sensitivity Analysis in Epidemic Modelling Using Polynomial Chaos (May, 2022)
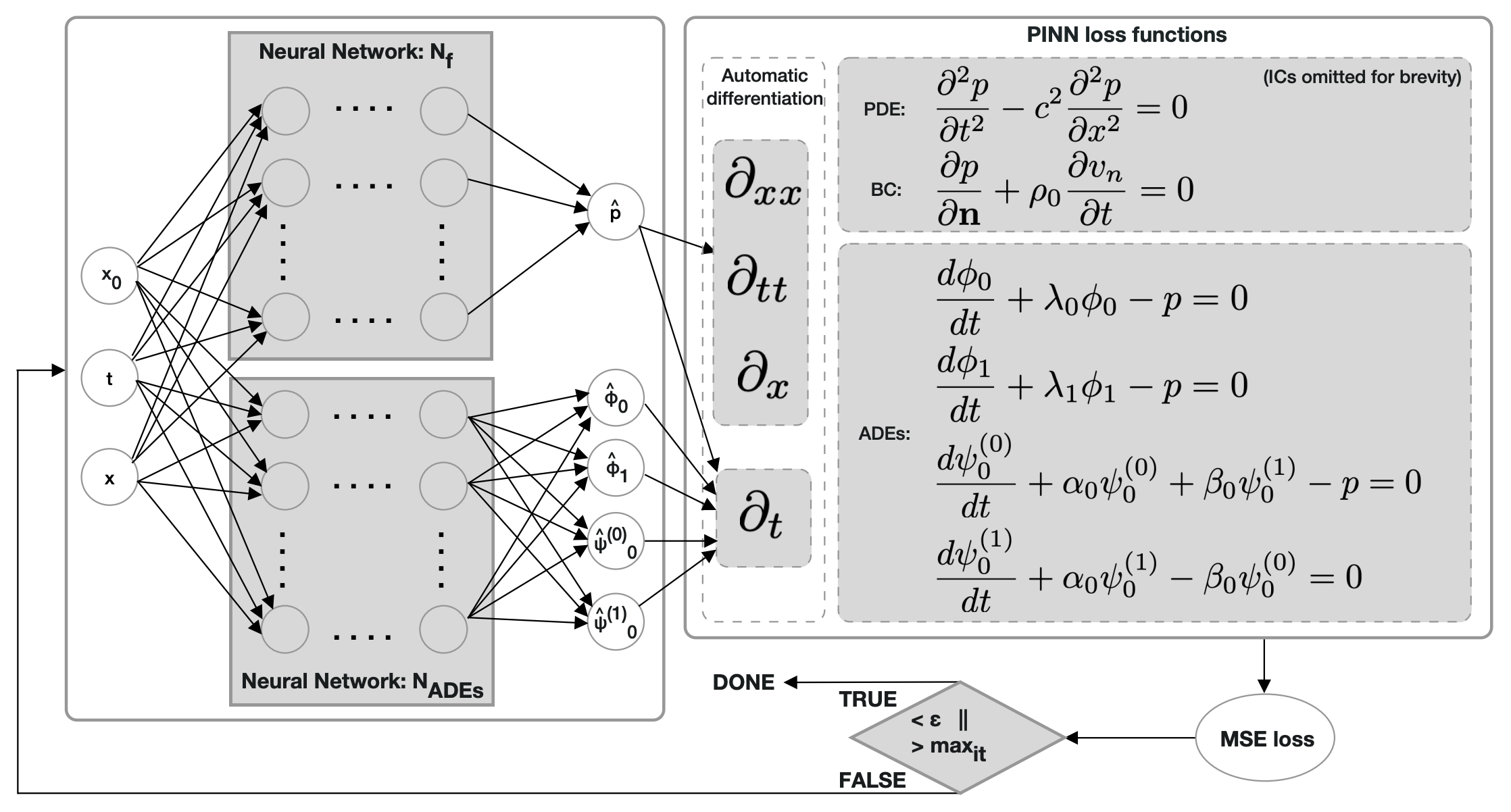
- Machine learning-based room acoustics using flow maps and physics-informed neural networks (Apr 2022)
- Physics-informed neural networks for one-dimensional sound field predictions with parameterized sources and impedance boundaries (Dec 2021)
- Assessment of the National Test Strategy on the Development of the COVID-19 Pandemic in Denmark (Nov 2021)
- Efficient p-Multigrid Spectral Element Model for Water Waves and Marine Offshore Structures (May 2021)
- Reduced Order Modeling for Nonlinear PDE-constrained Optimization using Neural Networks (Apr 2019)
- A massively scalable distributed multigrid framework for nonlinear marine hydrodynamics (Feb 2019)
- Spectral Tensor-Train Decomposition (2016)
Other publications / preprints / reports
- Physics-Informed Holomorphic Neural Networks (PIHNNs): Solving Linear Elasticity Problems (July, 2024)
- A sensitivity analysis on the effect of hyperparameters in deep neural operators applied to sound propagation (2023, Forum Acousticum, proceedings)
- Sound propagation in realistic interactive 3D scenes with parameterized sources using deep neural operators (August, 2023, submitted)
- Improving deep learning-based defect classification in solar cells using conformal prediction (January, 2023, XXX, proceedings)
- Enabling Interactive Virtual Reality for Room Acoustics in Enclosed Spaced Using Numerical Methods (October, 2022, ICA 2022, proceedings)
- DeepONet: Learning the sound propagation in 1D with parameterized sources using deep learning for approximating the wave equation operators (October, 2022, ICA 2022, proceedings)
- Accelerating hydrodynamic simulations of urban drainage systems with physics-guided machine learning (June 2022, preprint))
- Machine learning-based room acoustics using flow maps and physics-informed neural networks (April 2022, submitted)
- Reduced Order Modelling for Dispersive and Nonlinear Water Wave Modelling (Jan 2022, submitted)
- Making Waves: How emerging physics-informed machine learning techniques can change established hydrodynamic modelling paradigms (Nov 2021, submitted)
- Physics-informed neural networks for 1D sound field predictions with parameterized sources and impedance boundaries (Sep 2021, preprint)
- Efficient Uncertainty Quantification and Sensitivity Analysis in Epidemic Modelling using Polynomial Chaos (Sep 2021, submitted)
- Efficient numerical room acoustic simulations with parametrized boundaries using the spectral element and reduced basis method (Mar 2021, submitted)
- Age-dependent Epidemic Modelling of COVID-19 using a Nodal Discontinuous Galerkin Method (Feb 2021)
Workshops / Summer schools
- 2020, Model Order Reduction Summer School (MORSS) 2020 organized by EPFL (Ecole polytechnique federale Lausanne), DTU - Technical University of Denmark, a Eindhoven University of Technology (EuroTech Universities Alliance)
Research and innovation projects
-
Scientific machine learning of environmental systems
(2023-2026)
PhD student Anton Sørensen (DTU Sustain / DTU Compute, co-supervisor) - Efficient Added Mass Calculations for Large and Complex
Floating Offshore Structures (2023)
PhD student, Jens Haakon Visbech Christensen (COWIFONDEN / DTU Compute, principal investigator, main supervisor) -
Interactive auditory virtual reality using reduced order
modeling (2022)
PhD student, Hermes Sampedro Llopis (DTU Electro / DTU Compute / Ecophon / Ramboll / Virsabi / Treble technologies / Danish Sound Cluster, co-supervisor)
RB-SEM virtual acoustics (proof-of-concept) -
Reduced Order Modelling based Scientific Machine
Learning (2021-2023)
PostDoc, Fatma Guler (DTU Compute / Bartin University / TUBITAK, main supervisor) -
Robust Surrogate Modelling for Antenna Design
Applications (2020-2023)
Industrial PhD student, Sabine Fie Hansen (DTU Compute / TICRA / EPFL, main supervisor) -
Accurate and Fast Auditory Virtual Reality Implementation (2019-2022)
PhD student, Nikolas Borrel-Jensen (DTU Electro / DTU Compute / Eindhoven University of Technology / EuroTech, co-supervisor)
PhD thesis: Accelerated methods fo\ r computing acoustic sound fields in dynamic virtual environments with moving sources, oral lecture (youtube)
New position: Software developer, Meta, Redmond - Estimation, Simulation and Control for Optimal Containment of COVID-19 (2020)
PostDoc, Kristian Meyer (DTU Compute / AAU / Novo Nordisk foundation, main supervisor)
Research Assistant, Anders Dalsgaard Melander (DTU Compute / AAU / Novo Nordisk foundation, main supervisor) -
Acoustic Virtual Reality for Architectural Design (2019-2022)
Industrial PhD student, Hermes Sampedro Llopis (DTU Electro / DTU Compute / EPFL / Ramboll // Ecophon, co-supervisor)
Talk given at the Model Order Reduction Summer School (MORSS) 2020: RB models for real-time wave-based virtual acoustics simulations -
Uncertainty Quantification for Engineering Applications (2011-2014)
PhD Student, Daniele Bigoni (DTU Compute, main supervisor)
PhD thesis: Uncertainty Quantification with Application to Engineering Problems
Position after PhD: PostDoc at Department of Aeronautics and Astronautics, Massachusetts Institute of Technology. Cambridge, USA
Gallery
Function Approximation using Smolyak Sparse Grid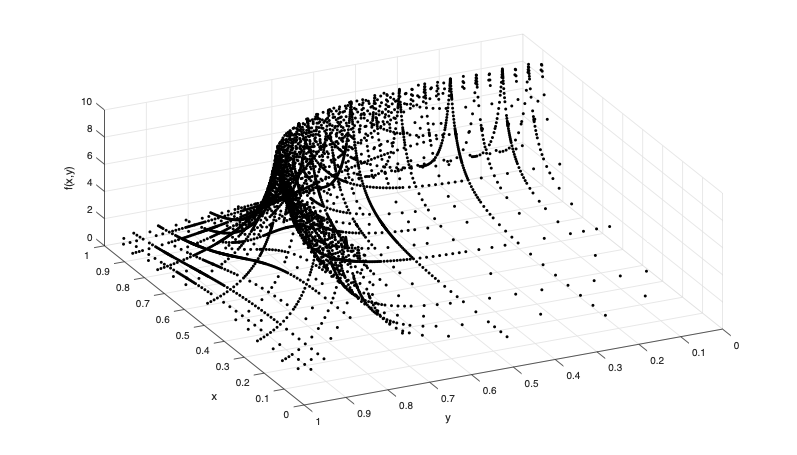 |
Function approximation using Spectral Tensor-Train
Decomposition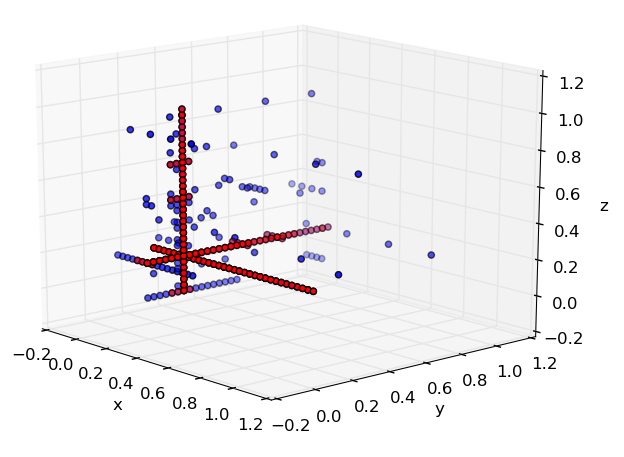 |
Real-time acoustic simulation in complex geometries using neural operator framework DeepONet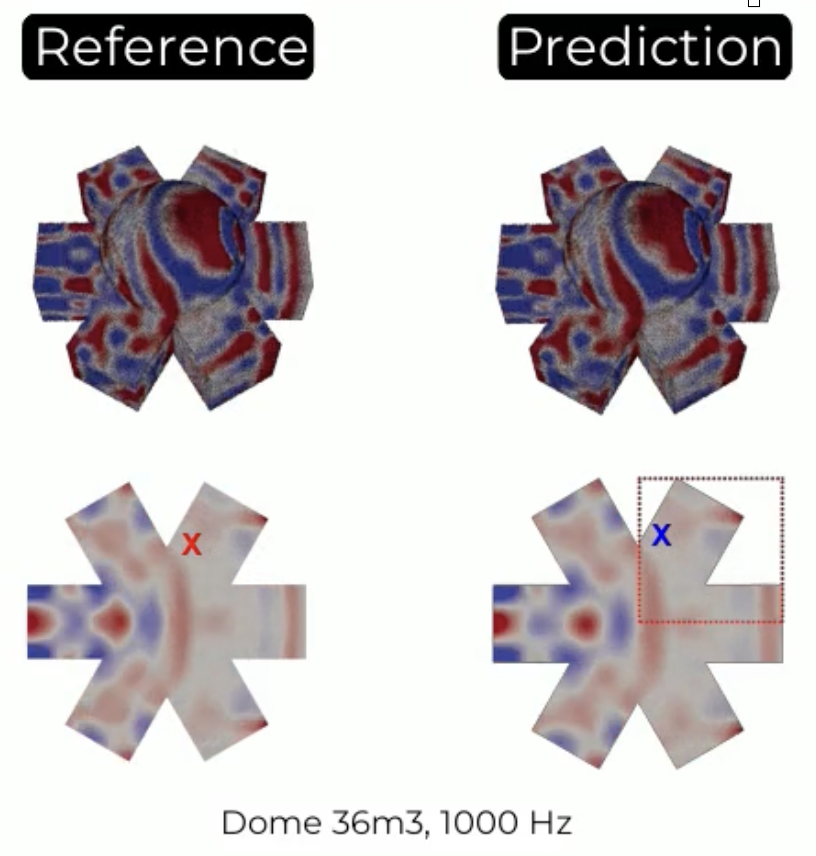
|
Fast acoustic simulations using reduced order modelling (ROM) vs full order models (FOM) for virtual environments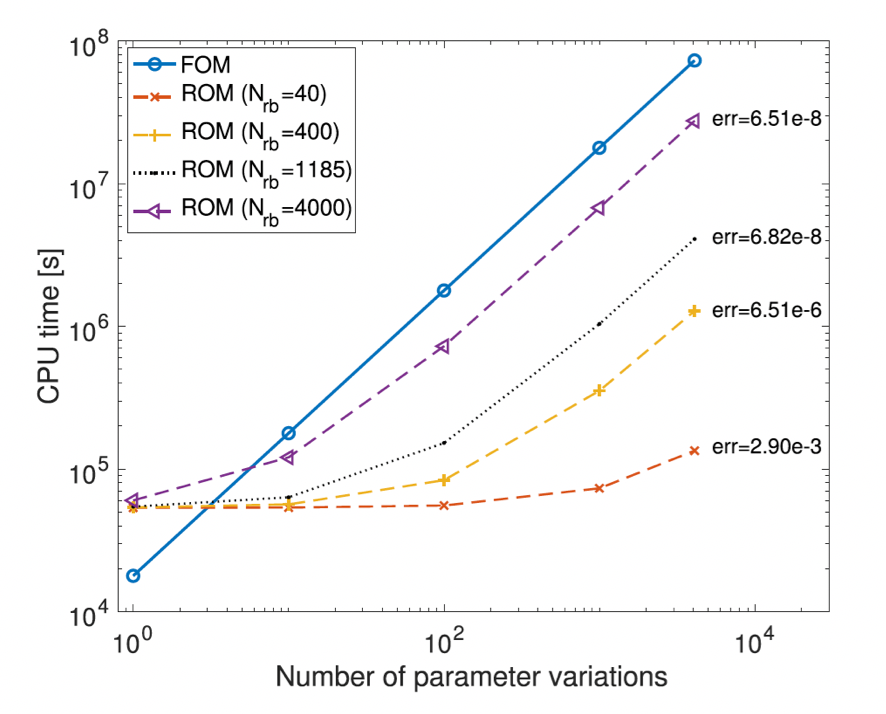
|
Efficient Uncertainty
Quantification using Spectral
Methods (Polynomial Chaos)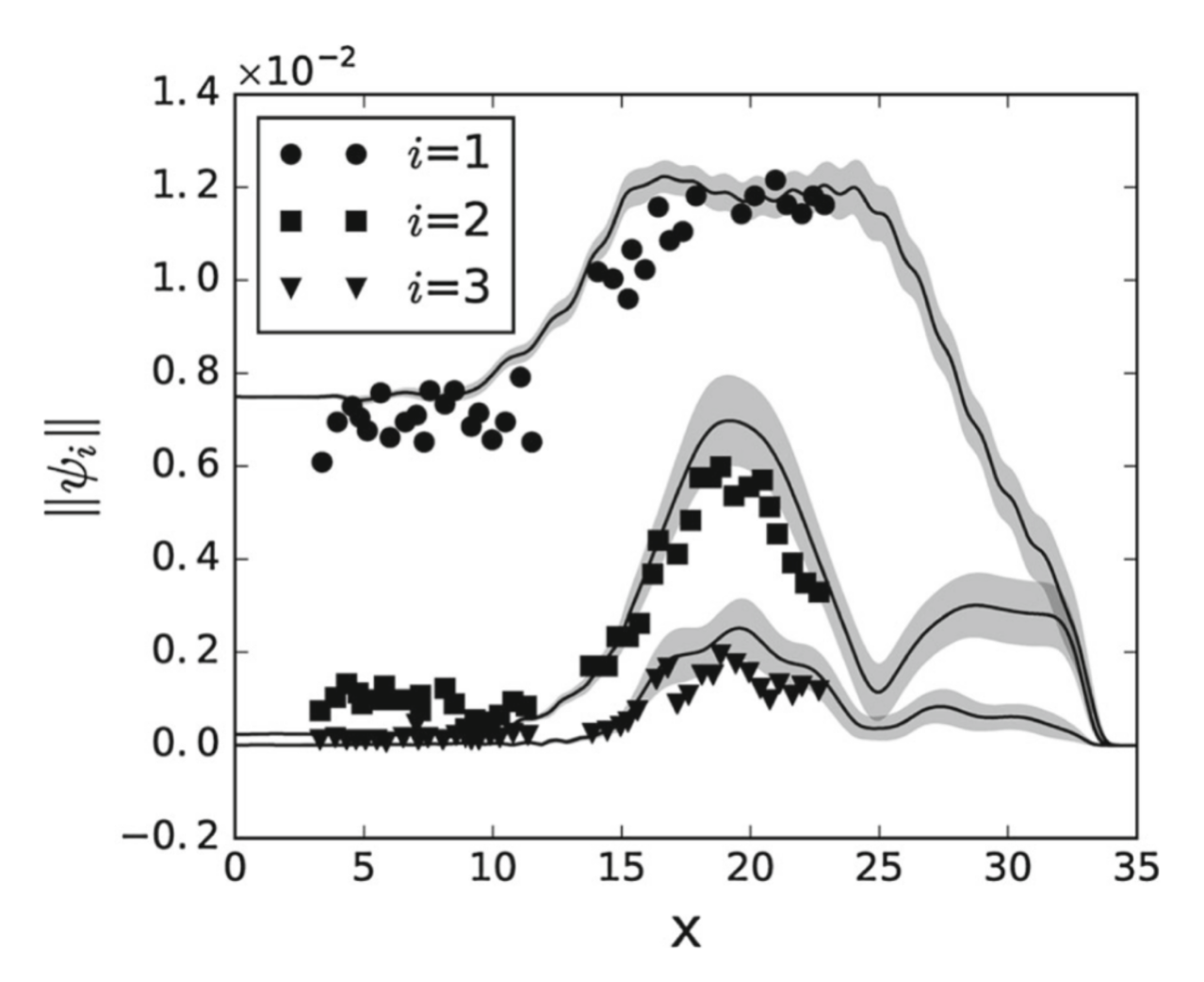 |
Massively parallel multi-GPU accelerated multigrid
methods for large-scale
simulations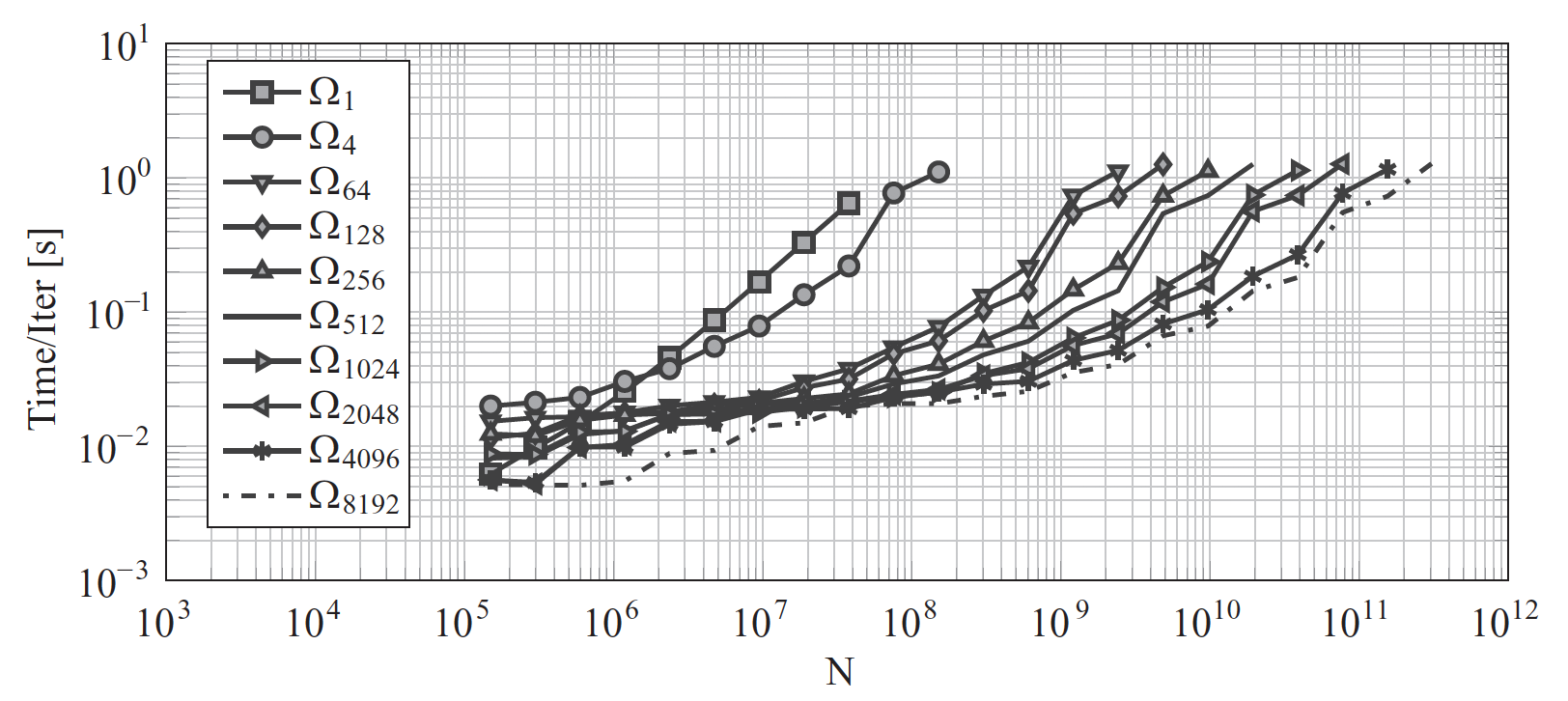 |
|
Anomaly detection using self-supervised learning |
|
Spectral Element Reduced Basis
Method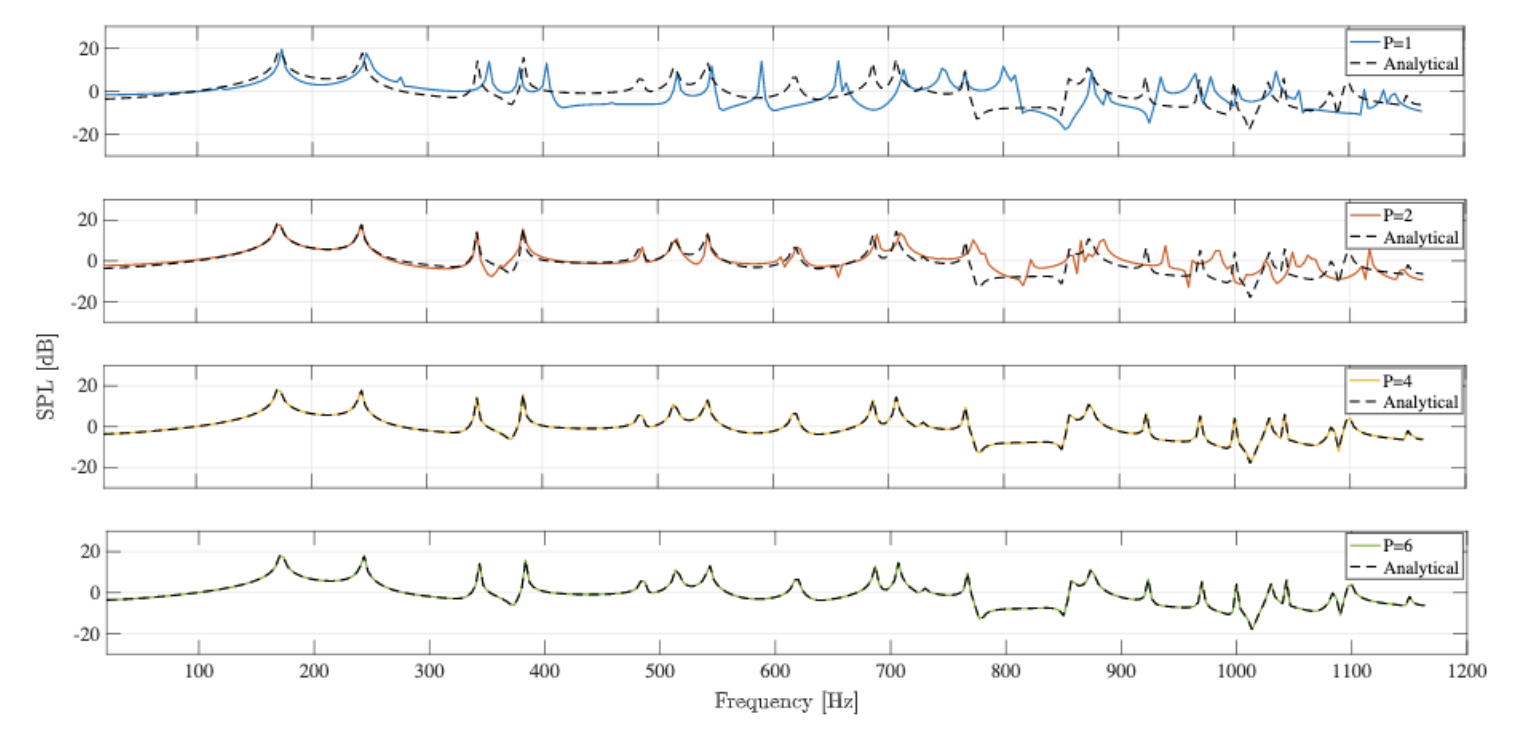
|
|
Physics Informed Neural Networks for Parameter Estimation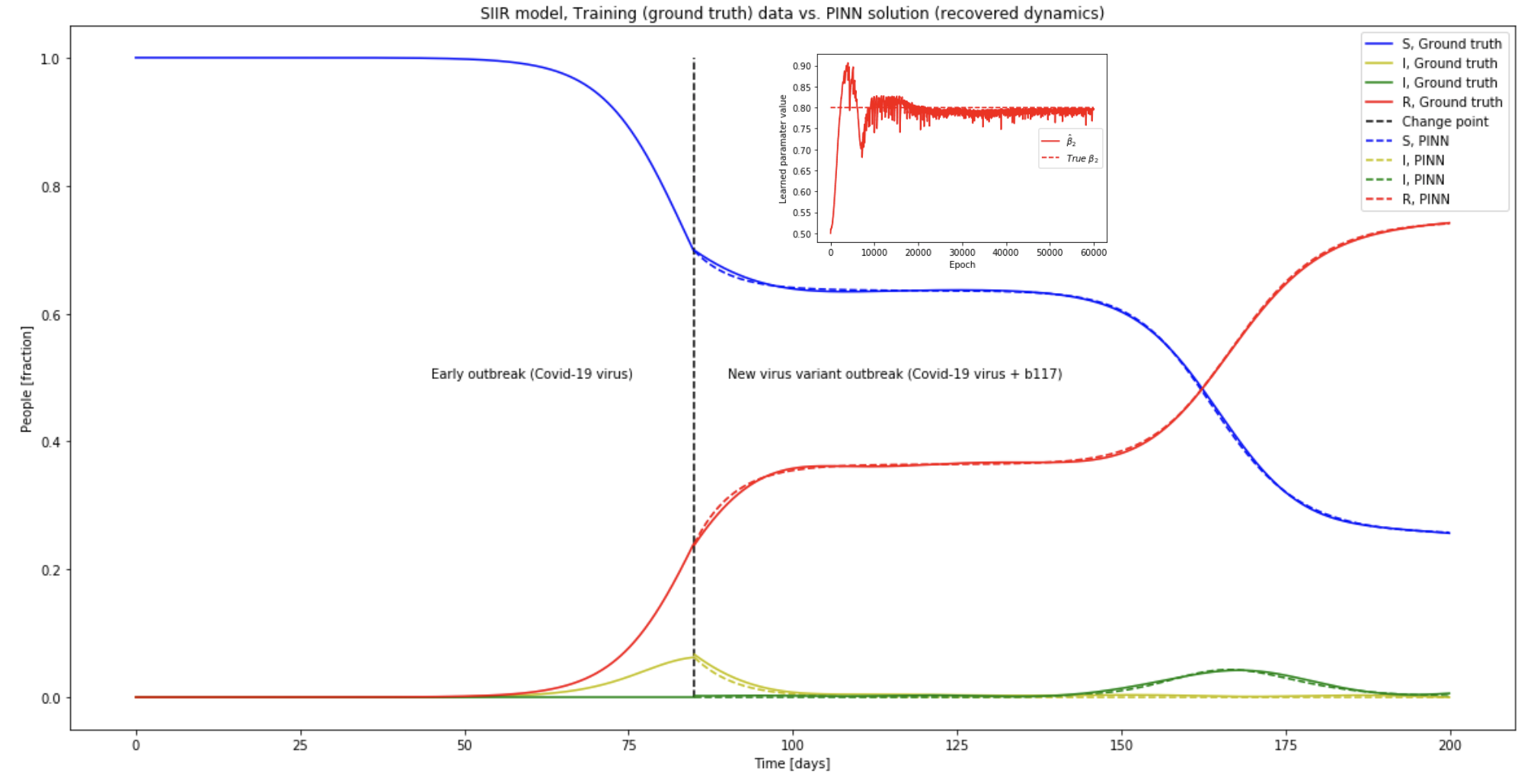
|
|
Adaptive Mesh Refinement Techniques
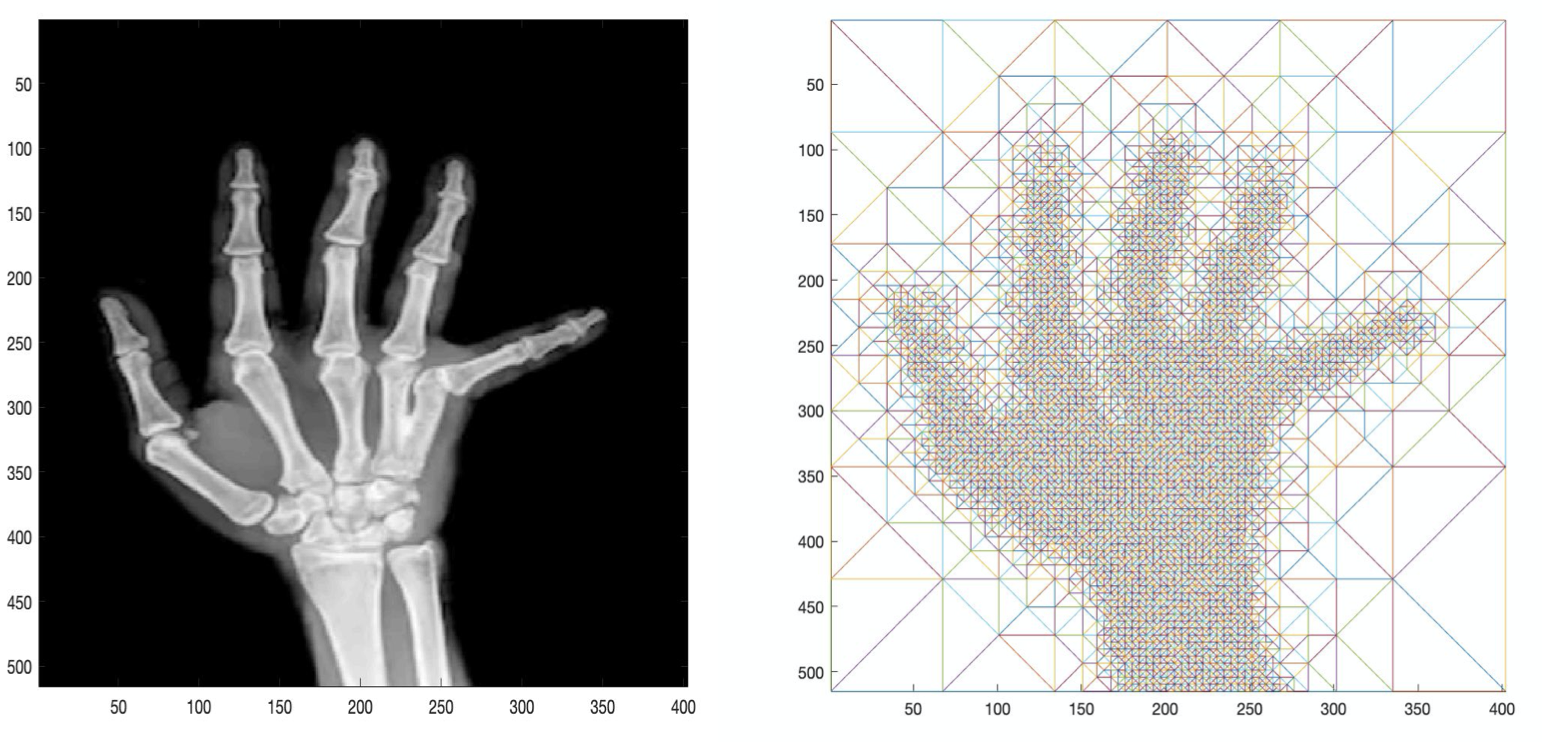
|
|
Neural Network Residual (ResNet) Arrchitetcures for Dynamical systems

|
|
Physics-informed neural network for Navier-Stokes equations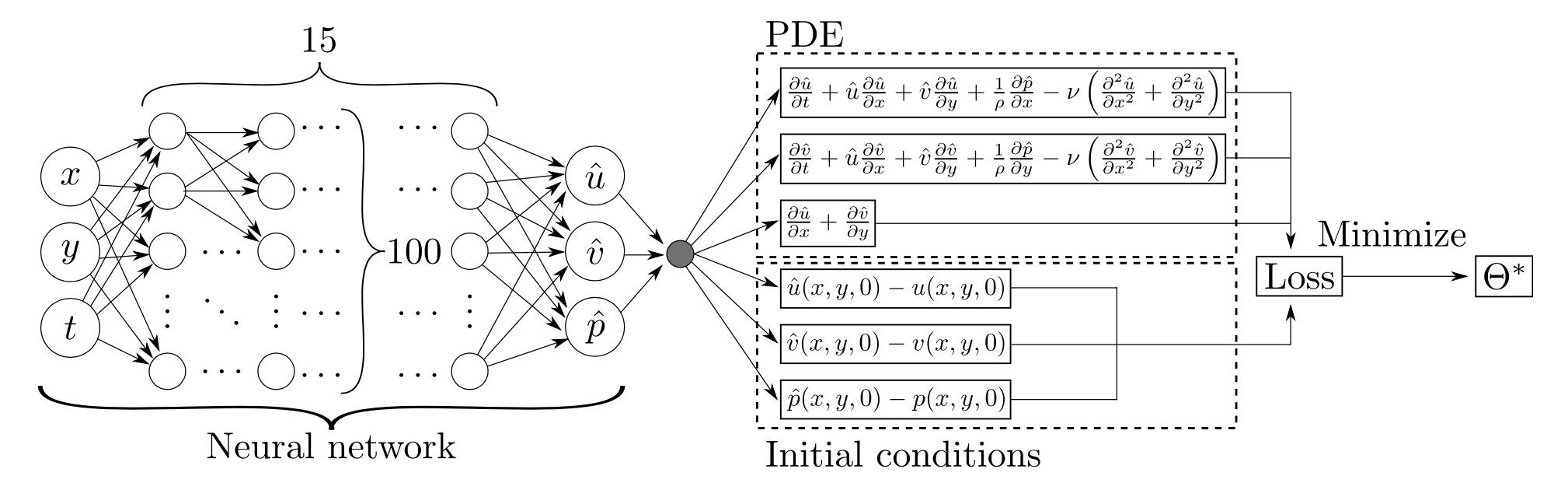
|
|
Physics Informed Neural Network for the Taylor Greeen Vortex
solution in computational fluid dynamics (CFD)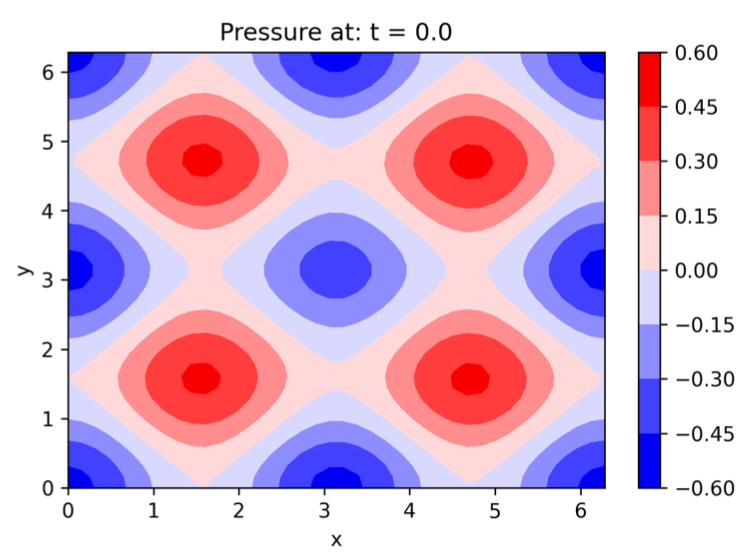
|
|
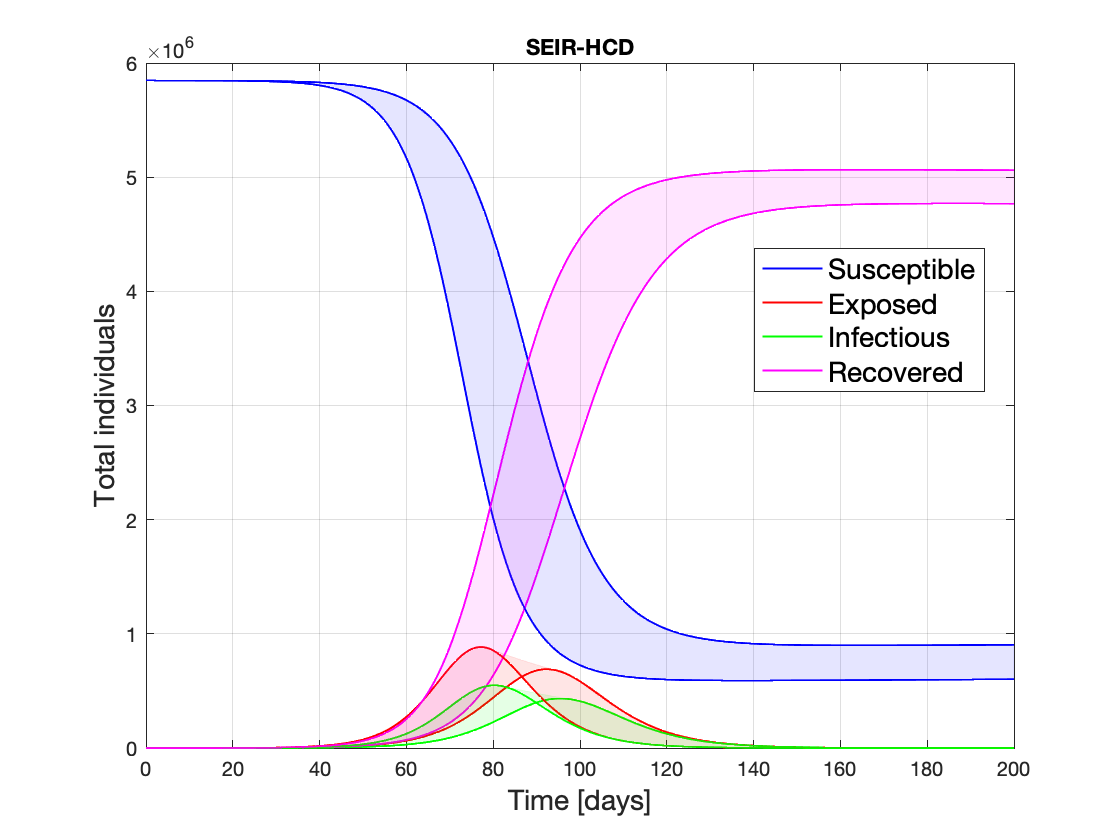
Data-driven physics-constrained real time estimation of effective transmission of the spread of covid-19 for Denmark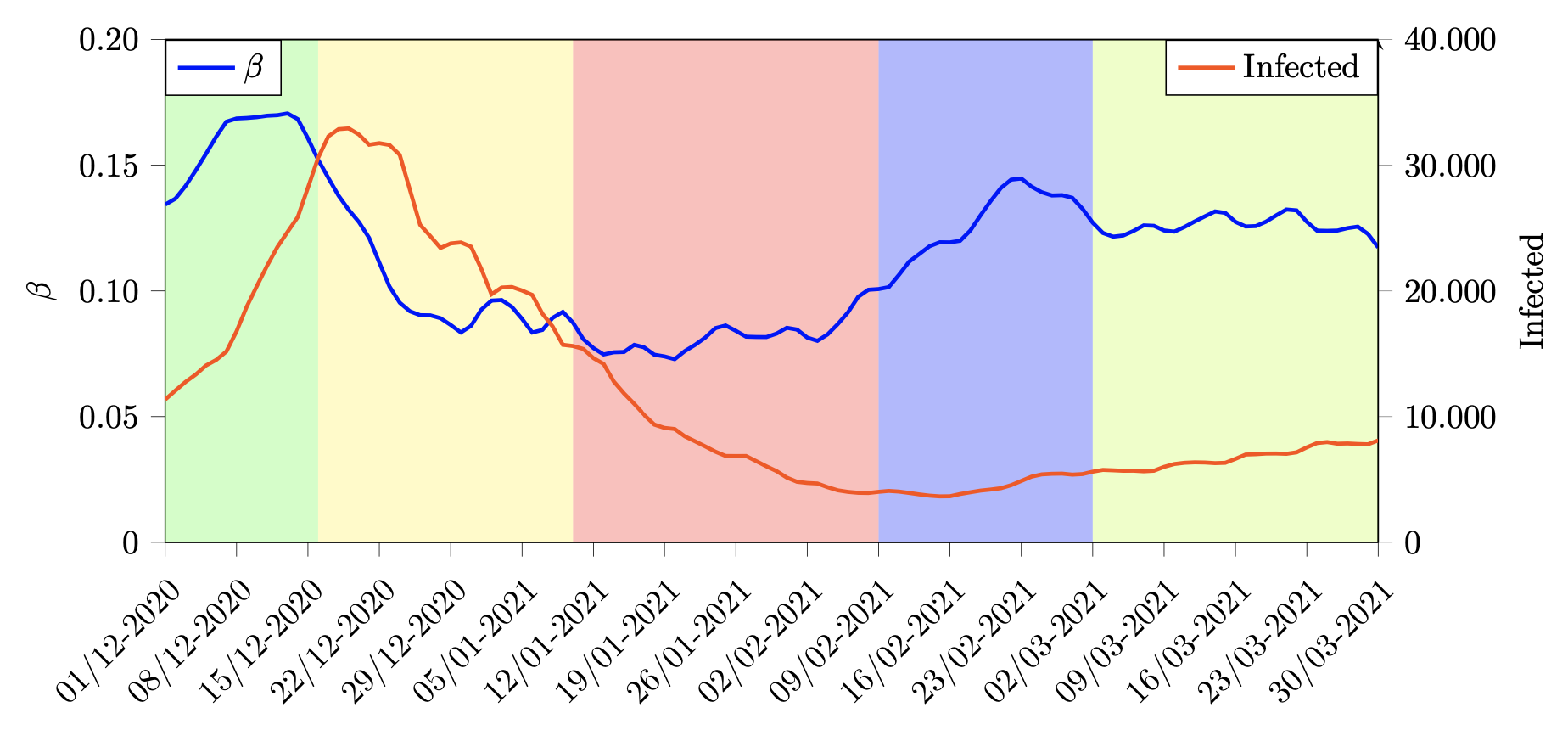
|
|
Deep Neural Networks for data-driven physics-constrained
simulation of a nonlinear coupled ODE system
|
|
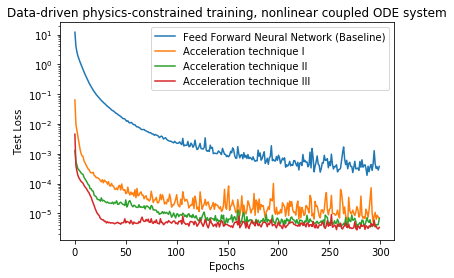
|
|
Low rank approximation and modelling from data using
dynamic mode decomposition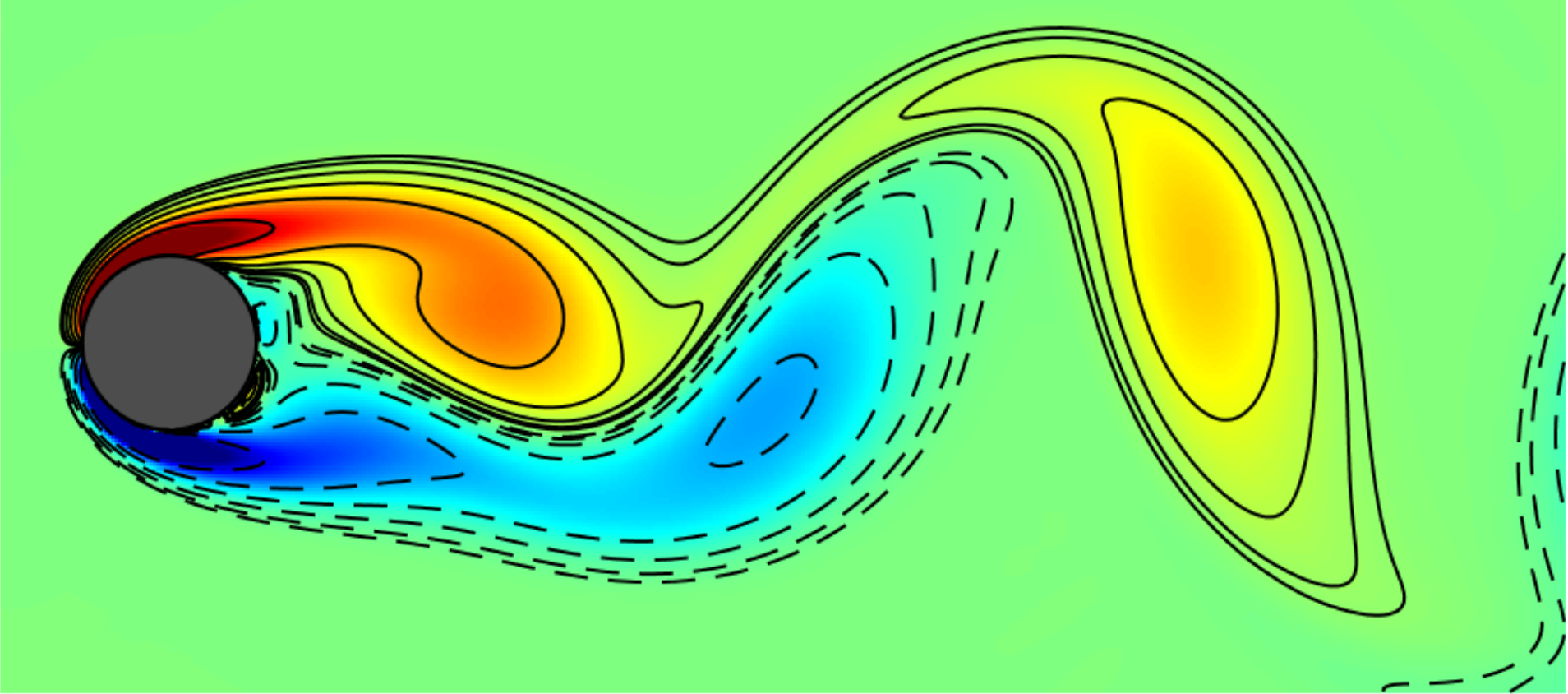
|
|
